超解像基礎から提案モデルまで ~深層学習AIによる画像の高解像度化~
応用編―エンジニア向けブログ
低解像度(Low-Resolution; LR)画像から高解像度(High-Resolution; HR)画像を再構成する技術
すなわち超解像(Super-Resolution; SR)の研究内容を詳細にご紹介します。


- ホーム > ブログ > 応用編 ―エンジニア向けブログ― >
2025年11月26日
超解像基礎から提案モデルまで ~深層学習AIによる画像の高解像度化~
目次
エイシングのリサーチ&デベロップメント部でスペシャリストとしてAI開発案件の担当やTransformerモデルの構築とそれによる異常検知などに取り組んでいます。
その立場から、テックブログというかたちで技術を深掘りしてお伝えできればと考えています。
はじめに
近年、ディープラーニング技術の発展により、画像の高精細化、すなわち超解像(Super-Resolution; SR)の研究が急速に進展しています。
超解像とは、低解像度(Low-Resolution; LR)画像から高解像度(High-Resolution; HR)画像を再構成する技術です。
この分野は、監視カメラ・医用画像・リモートセンシング・産業検査など、あらゆる場面で高精細な情報を必要とするタスクにおいて重要な位置を占めています。
筆者は、これまでにCNNを用いた一般的な超解像手法を学びつつ、独自にエッジ抽出とグレースケール情報を利用した段階的超解像モデルを提案しました。
本記事では、まず超解像技術の理論的背景と従来手法を整理し、その後、筆者の研究内容を詳細に紹介します。
1. 超解像とは何か
1.1 超解像の目的と定義
超解像は、欠損情報を再推定する逆問題の一種です。
低解像度画像は、以下のように表現できます。
$$
I_{LR} = D(B(I_{HR})) + n
$$
ここで、
- \(I_{HR}\) :本来の高解像度画像
- \(B( \cdot )\) :ぼかし(Blur)作用
- \(D(\cdot)\) :ダウンサンプリング作用
- \(n\) :観測ノイズ
つまり、超解像とはこの式を逆にたどって、
$$
I_{HR} \approx f_{\theta}(I_{LR})
$$
という関数(ニューラルネットワークなど)を学習する問題といえます。
LRからHRへの変換イメージは以下の図のようになります。

図1: 超解像のモデルイメージ
1.2 シングルイメージ超解像(SISR)とマルチイメージ超解像(MISR)
超解像には主に2つの種類があります。
| 分類 | 概要 |
|---|---|
| SISR | 1枚のLR画像からHR画像を再構成。深層学習研究の主流。 |
| MISR | 複数のLR画像(視点や時間が異なる)を統合してHR画像を生成。計算コストが高いが精度は高い。 |
今回の内容では、SISRに焦点を当てて説明していきます。
2. 従来の補間ベース超解像
深層学習が登場する以前、画像の高解像度化はデータの学習を行わないリサイズアルゴリズム(補間法)に依存していました。
ここでは代表的な手法を数理的に整理します。
2.1 Nearest Neighbor
最も単純な補間法。
新しい画素の値を最も近い既存画素の値にコピーします。
$$
(求める点) = I(\text{round}(x), \text{round}(y))
$$
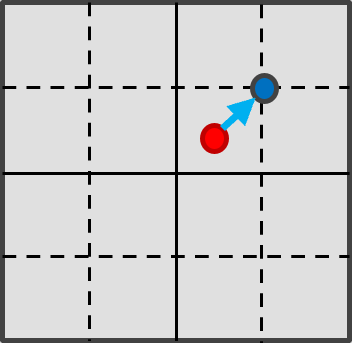
図2: Nearest Neighbor
利点:高速・実装容易
欠点:ジャギー(ギザギザ)が発生しやすい
2.2 Bilinear
周囲4点の画素値から線形補間します。
$$
x=i*(1-a) + j*a, target=x*(1-b) + y*b
$$
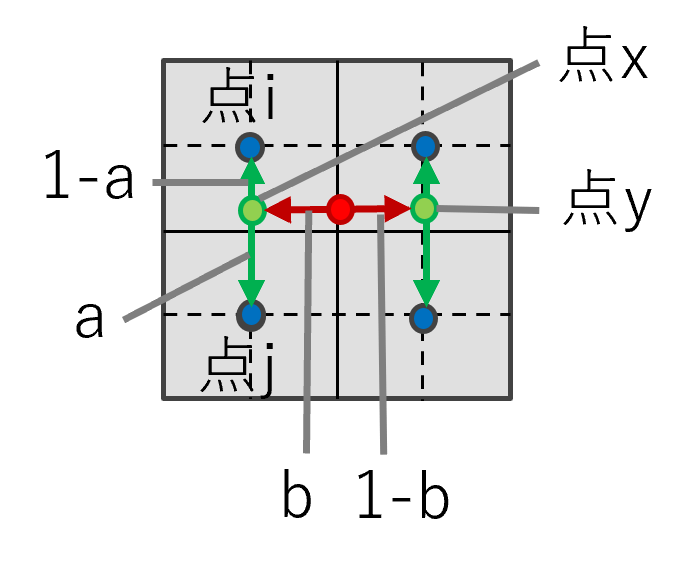
図3: Bilinear
利点:滑らか
欠点:ぼやけやすく、エッジが失われる
2.3 Bicubic
さらに広い範囲(4×4=16画素)を用い、三次式で近似して補間します。
$$
I'(x, y) = \sum_{i=-1}^{2}\sum_{j=-1}^{2} w(i, j) I(x+i, y+j)
$$
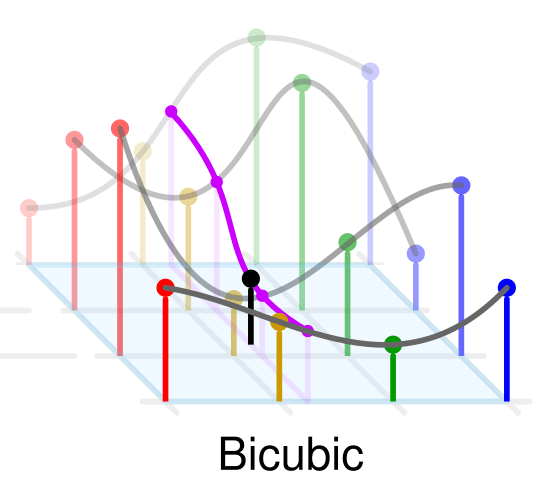
図4: Bicubic(wikipediaより)
以下、OpenCVを使って各補完法を実装した場合の比較です。Nearest Neighbor → Bilinear → Bicubicの順に出力が綺麗になっていくことがわかります。

図5: 補間法による出力の比較
3. 深層学習による超解像の発展
3.1 SRCNN(2016)
DongらによるSRCNN[1]は、初めてCNNを用いた超解像モデルとして知られています。
手順は次の通りです。
- 入力画像をBicubic補間で拡大
- CNNで高周波成分を再構成
- 損失関数MSE Lossを用いて学習
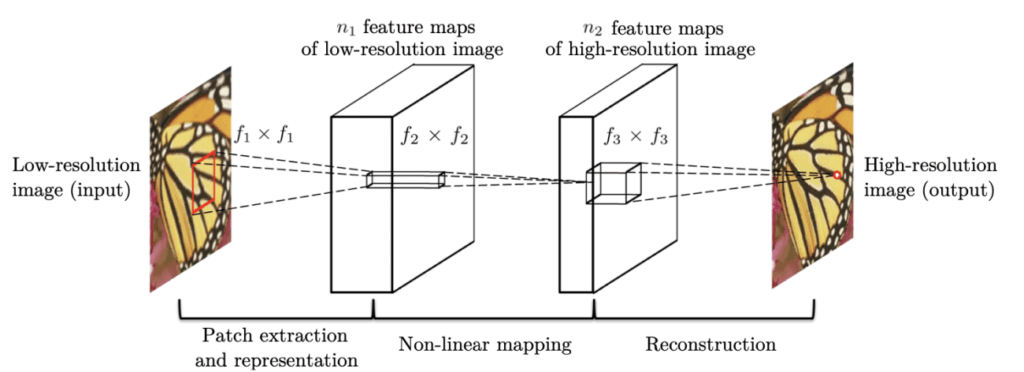
図6: SRCNN概要図(原論文より)
畳み込みニューラルネットワーク(CNN)の構造や畳み込み処理(Convolution)をまだ知らない方は、前回の「画像認識ニューラルネットワークとは?」の記事で解説しましたので参考にしてください。
3.2 Transposed Convolution(Deconvolution)
SRCNNでは補間後の画像を入力にしていましたが、小領域から拡大を行う逆畳み込み(Deconvolution)を用いると、学習可能なアップサンプリングが可能になります。ただし、逆畳み込みによる重なり部分が発生するため「Checkerboard Artifact」と呼ばれるノイズが発生する問題がありました。

図7: DeconvolutionとCheckerboard Artifact[2]
3.3 ESPCN(Pixel Shuffler)
この逆畳み込みによるCheckerboard Artifactを解決するために提案されたのがPixel Shuffler[3]という手法です。Pixel Shufflerは、ESPCNというモデルで提案された手法になります。仕組みとしては、畳み込みにより\(r^2\)枚の特徴量チャンネルを生成し、それを1チャンネルに並べ直して\(r \times r\)倍に拡大した画像を生成するというものです。これによって逆畳み込みによる領域の重なりがなくなるため、Checkerboard Artifactを発生させることなく画像を高解像度化することができます。
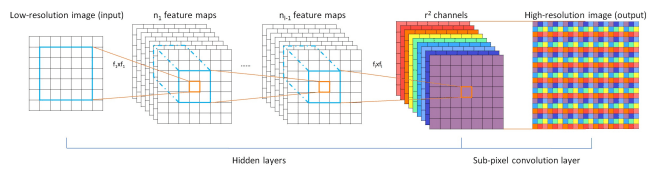
図8: PixelShuffler(原論文より)
4. 精度評価指標
超解像では主に以下の2つの指標を使って高解像度化の精度を測ります。
4.1 PSNR(Peak Signal-to-Noise Ratio)
平均二乗誤差(MSE)に基づく定量指標です。
以下の計算式によって定義されます。
$$
PSNR = 10 \log_{10}\left(\frac{MAX^2}{MSE}\right)
$$
値が高いほど復元精度が高いですが、人間の主観評価とは必ずしも一致しないというデメリットがあります。MSEを使って計算するので画像がぼやけていても全体の雰囲気さえ似ていればそこそこ良い値が出てしまうためです。
4.2 SSIM(Structural Similarity Index Measure)
構造的類似度を考慮した評価指標です。以下の計算式によって定義されます。
$$
SSIM(x, y) = \frac{(2\mu_x\mu_y + C_1)(2\sigma_{xy} + C_2)}{(\mu_x^2+\mu_y^2 + C_1)(\sigma_x^2+\sigma_y^2 + C_2)}
$$
画像の輝度・コントラスト・構造を元に、ピクセルごとにその周辺の平均、分散、共分散を使って類似度を計算します。PSNRに比べてこちらの方が人間の感覚に近い指標と言われています。
4.3 PSNRとSSIMの比較
以下がPSNRとSSIMの比較例です。
右上が左画像を全体を均等に明るくした場合、右下が左画像の各ピクセルをランダムに明るくしたり暗くした場合の画像です。
人間の感覚的には、左画像と右上の画像は綺麗に変換されていて類似度が高いように見え、左画像から右下の画像へは荒い画質に変換されているように感じます。
しかしながら、この変換において、MSE(PSNR)の値はどちらの変換も同じである一方、SSIMの値は右上の画像の変換の方が高い数値を示しています。
このように、PSNRは画像全体の類似度を表す一方で、SSIMは画像の構造的な類似度を表すという特徴があります。
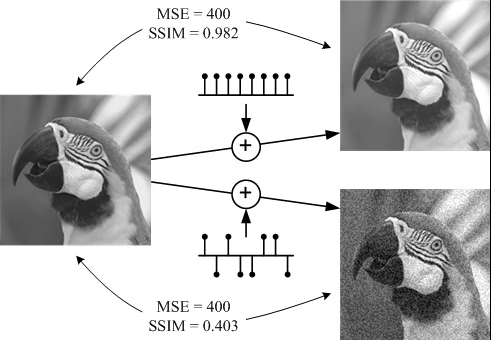
図9: PSNRとSSIMの比較例[4]
5. 提案手法:エッジとグレースケール画像を用いた段階的超解像
5.1 背景と目的
従来のCNNベースの超解像では、損失関数にMSE Lossを使用して画像全体の類似度を測っているため、超解像後の画像がぼやけてしまうという問題点がありました。
筆者はこの問題を解決するために、エッジ成分とグレースケール情報を独立に学習し、段階的に統合する構造[5]を提案しました。提案モデルの構造は以下のようになっています。
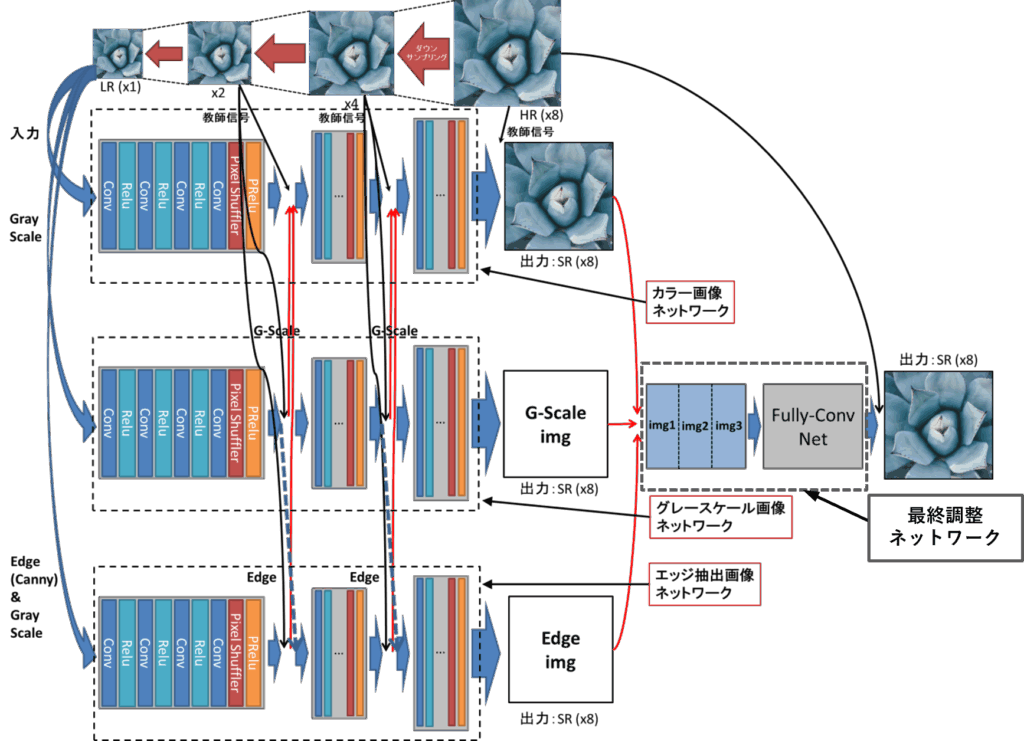
図10: 提案モデル図
5.2 モデル構成
提案モデルは以下の3系列のネットワークで構成されています:
- カラー画像ネットワーク(Color SR)
通常のRGB画像を入力とし、全体的な色調と構造を学習。 - グレースケール画像ネットワーク(Gray SR)
輝度情報に特化し、明暗の階調表現を強化。エッジネットワークで処理されるエッジ画像を補完。 - エッジネットワーク(Edge SR)
Canny法で抽出したエッジ画像を入力とし、輪郭・境界を再構築。
各ネットワーク構造は以下のようになっています。
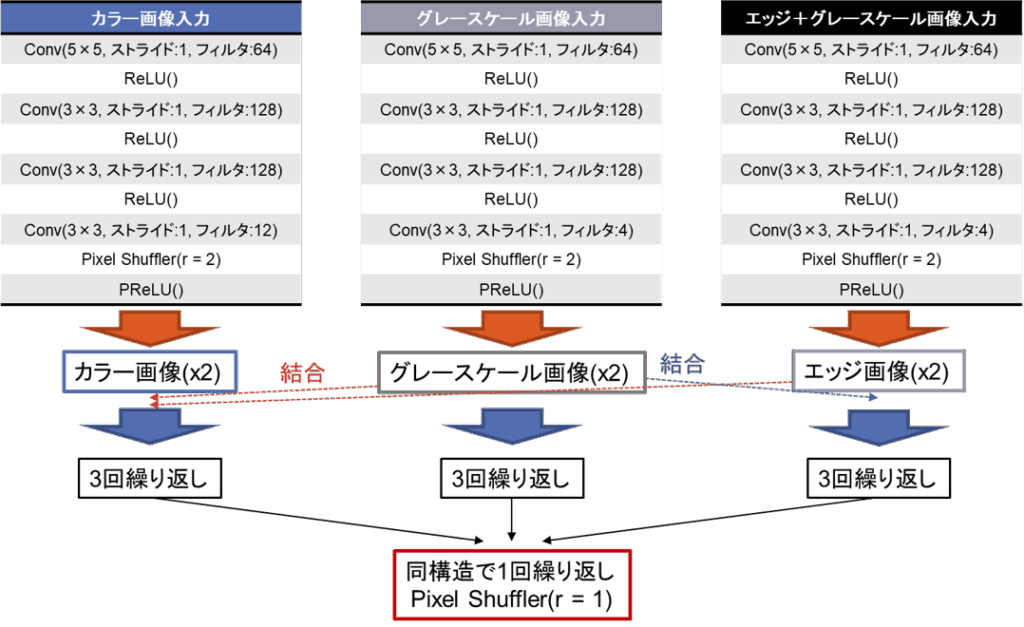
図11: モデルネットワーク構造
5.3 データ処理とモデル学習
- 元画像から順にダウンサンプリングして x2, x4, x8 の段階データを作成。
- 各段階で個別にSRネットワークを学習。
- 各出力をカラー画像ネットワークの出力に統合し、次段階の入力に反映。
- グレースケール画像ネットワークの各出力をエッジ画像ネットワークの出力に統合し、次段階の入力に反映。
- 最終段階(x8)でカラー・グレースケール・エッジ画像を結合し、全体最適化を実施。
5.4 本提案モデルの目的
- MSEによって出力画像がぼやけてしまうため、エッジ情報で物体の境界線を補正し、よりシャープな結果を得る。
- 段階的学習によりx8のような高倍率拡大に対して安定した学習を実現。
6. 実験結果
6.1 超解像処理による検証
本実験では、Sun-Hays80という自然画像80枚の超解像用データセットを使用して検証を行いました。結果として、以下のような出力が得ることができました。これらの結果から、入力画像に比べて物体の境界がはっきりする形で画像が高解像度化されていることがわかります。

図12: 入出力画像1

図13: 入出力画像2
6.2 PSNR・SSIM比較(x8)
以下のグラフはモデルの学習過程による検証データのPSNRとSSIM値です。Sun-Hays80データセットを使用し、学習データ73枚、検証データ7枚で精度検証を行っています。
赤色のグラフが提案モデル、青色のグラフがカラー画像ネットワークのみのモデル、紫色のグラフが従来法のSRCNNの学習過程での精度変化です。
| モデル | PSNR | SSIM |
|---|---|---|
| 提案モデル | 高 | 高 |
| カラー画像ネットワークのみモデル | やや高 | やや高 |
| 従来モデル(ダウンサンプリングなし) | 低 | 低 |
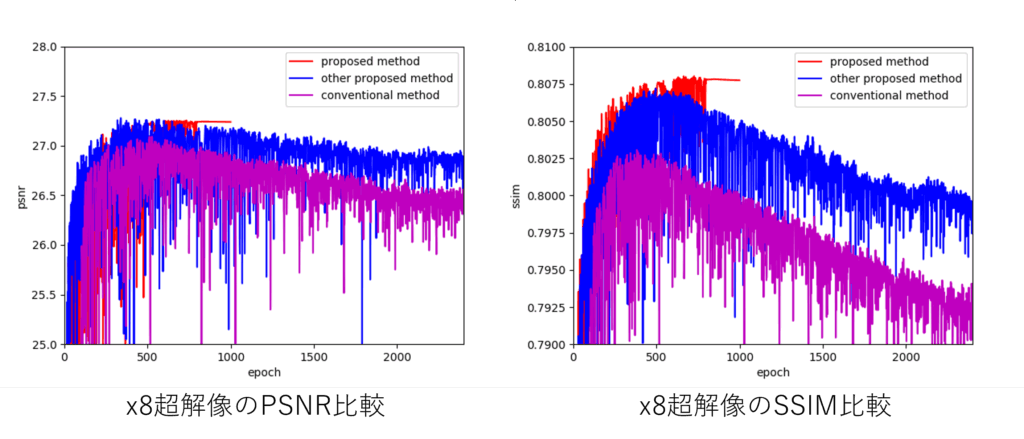
図14: PSNR/SSIM比較
この結果から、グレースケール画像ネットワークとエッジ画像ネットワークを導入することで、超解像の精度向上、収束速度の向上、過学習の抑制効果が得られていることがわかります。また、SSIM指標において特に精度が向上していることがわかります。
6.3 各段階の超解像精度推移
また、以下はSun-Hays80データセットにおける各段階でのSSIMの検証データの精度推移です。このx2~x8まででSSIM値自体は徐々に低下し、最終調整のネットワークによる処理を行っても精度がほぼ変化していないことがわかります。
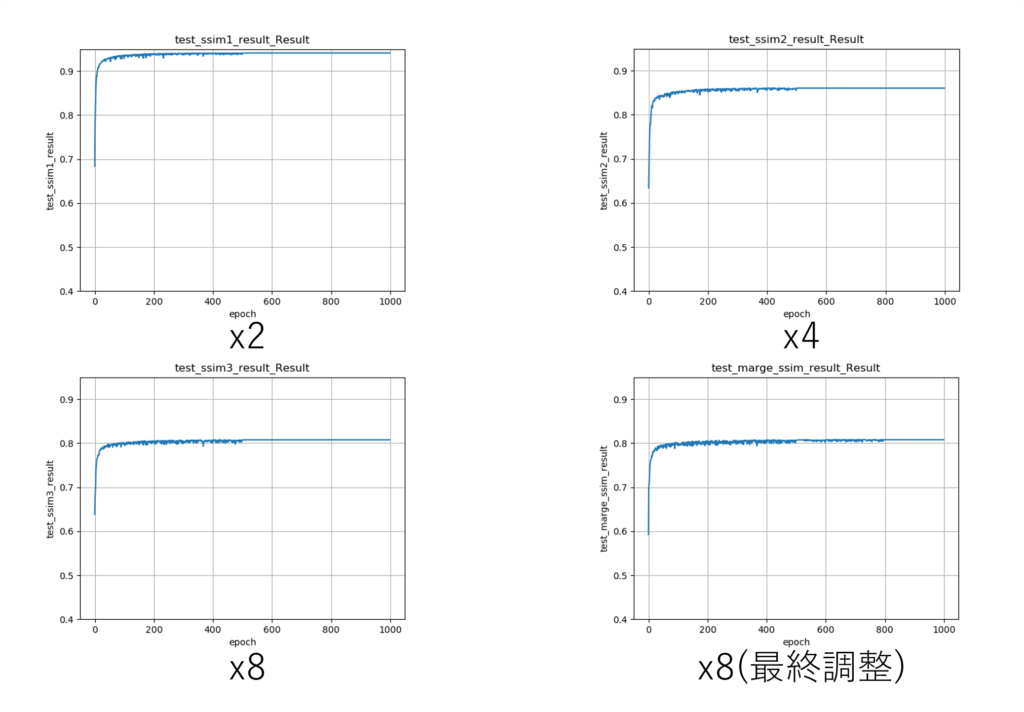
図15: 各段階におけるSSIM精度推移
7. 考察
段階的な超解像処理が高倍率での超解像精度の向上に寄与しているのを確認しました。また、エッジ画像ネットワークとグレースケール画像ネットワークを導入することでSSIM値の向上を確認しました。これにより、エッジ画像ネットワークがMSE由来のぼやけを補正し、グレースケール情報が輝度の滑らかさを保持に寄与したのではないかと考えています。一方で最終調整のネットワークを導入しても超解像精度の向上は見られませんでした。
8. 超解像技術の応用先
超解像技術の応用先の例としては、低解像度画像から高精度なエッジ抽出を行うことによる工業製品の寸法計測補正があります。例えば、本提案モデルを用いてx8の超解像を適用したい場合、学習データとしては、寸法計測したい対象物を同じ視点から低解像度カメラと高解像度カメラで撮影した画像が必要になります。具体的には、モデルに入力したい解像度の低解像度画像、低解像度画像に対して2倍の高解像度画像、4倍の高解像度画像、8倍の高解像度画像の計4種となります。これらの画像を最低80セット程度モデルに学習させることで、超解像処理を行うモデルを作成することができます。超解像モデルを作成した後は、エッジ画像ネットワークの出力画像を取り出す、または、カラー画像ネットワークの出力画像にエッジ抽出をかけることで、低解像度画像から高解像度なエッジ画像を生成することができます。この高解像度エッジ画像を寸法計測用の機器やアルゴリズム等と組み合わせることで、従来手法による寸法計測を補正することができます。
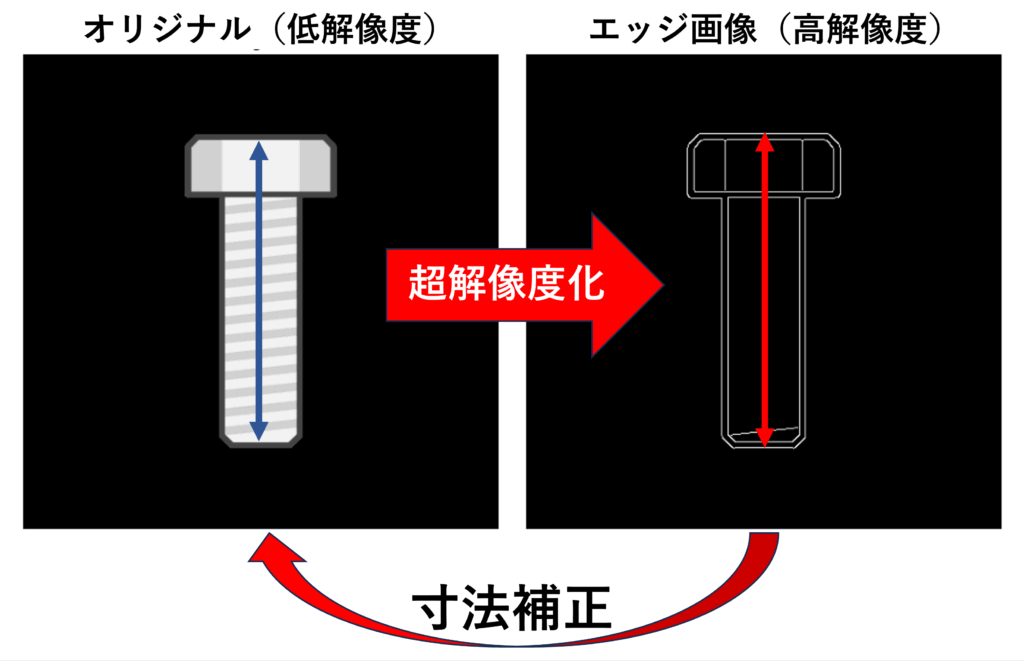
図16: 超解像エッジ抽出による補正
まとめ
本記事では、超解像技術の基礎から従来法、そして筆者の提案する「エッジとグレースケール画像を用いた段階的超解像」について解説しました。
今後はGAN等を含む競争的学習手法の導入により、より自然で高精細な超解像を目指します。
📚 参考文献
[1] Dong, C. et al., “Image Super-Resolution Using Deep Convolutional Networks (SRCNN),” IEEE TPAMI, 2016.
[2] Odena, A. et al., “Deconvolution and Checkerboard Artifacts” ( https://distill.pub/2016/deconv-checkerboard/ )
[3] W. Shi. et al., “Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network,” arXiv:1609.05158, Sep. 2016.
[4] Wang, Z. et al., “Mean Squared Error: Love It or Leave It? A New Look at Signal Fidelity Measures” (https://ece.uwaterloo.ca/~z70wang/publications/SPM09_figures.pdf)
[5] 平田大貴, 高橋規一, “エッジ画像とグレースケール画像を用いた段階的超解像モデル,” 電子情報通信学会総合大会講演論文集, 2021年.

